TOC
最初の課題：モーターの制御
マイクロマウスのソフトウェアで最初のマイルストーンとなるのがモーターの制御でしょう。 モーターの回転を滑らかに制御できるようになることが、スムーズな走行の基礎となるからです。 とりあえず左右のモーターそれぞれに移動速度を指定してやると、指定値に追従することを目標としてみます。
DCモーターの基本
そもそもDCモーターについてよくわかっていなかったので調べたところ、およそ二つの面があるようです。
- 流れる電流に比例するトルクを生み出す
- 回転数に比例して電圧（逆起電力）が生じる
電流と電圧はお互いに影響を及ぼしあってはいますが、まったく別のものです。 （純粋な抵抗のようにで電圧と電流が比例するような単純な関係にはなりません。） 例えばトルクはかかっているが軸は回転していないという状況では、電流は流れているが逆起電力がゼロになります。 逆に、理想的な無負荷状態では、軸の回転を維持するのにトルクが必要ありません。 この場合は電流はゼロでも逆起電力はゼロとなりません。 現実的にはモーターの軸に何も接続しない無負荷状態がこれに近く、モーターの摩擦トルクと釣り合う分以外の電流は必要ありません。
DCモーターの電気的な等価回路は以下のようにインダクタ、抵抗、電圧元が直列になった単純なものだそうです。
（DCモータを使ったマイクロマウス入門③から引用）
このうち、コアレスモーターの場合、インダクタンスLは小さいので無視してよいらしいです。
Rはモーターの巻き線抵抗、Eは回転数に比例する逆起電力です。
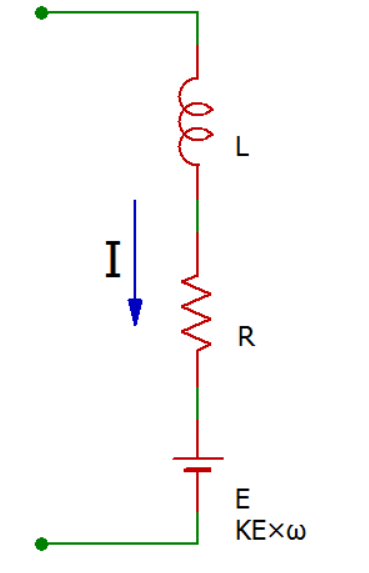
逆起電力$E$は回転数$ω$と逆起電力定数$K_E$によって $$ E = K_E\omega $$ と表されます。
また、軸に生じるトルク$T$はトルク定数$K_T$と電流$I$によって $$ T = K_TI $$ と表されます。
この逆起電力定数とトルク定数は、モーターの電力・運動エネルギー変換器という機能の効率を電気的・力学的それぞれの側面から見たもので、 本質的に同じものを表現しています。 数式としても等価で、 $$ K_E [\mathrm{V/rpm}] = \frac{2\pi}{60}K_T [\mathrm{Nm/A}] $$ と変換されます。（右辺の分母にある60というのはrpmに変換する際に混ざった60秒が由来です。）
フィードフォーワード制御のための計算
モーターをフィードフォーワード制御するために、望みの速度、加速度のときにモーターに与えるPWM制御のデューティー比を計算しましょう。 デューティー比を$r_D$、バッテリー電圧を$V_{bat}$とします。 モーターの両端の電圧$V_{mot}$はインダクタンスが無視できるので、 $$ V_{mot} = IR + E $$ となります。 この電圧がバッテリー電圧のデューティー比倍に等しいので $$ V_{mot} = r_D V_{bat} $$ 以上の式を連立してデューティー比を求めると $$ r_D = \frac{RT/K_T + K_E\omega}{V_{bat}} $$ という式が得られます。
ここで回転数$\omega$とトルク$T$はそれぞれ機体の速度と加速度に比例します。 この関係を数式で表すと、$v$を機体速度、$a$を機体加速度、$r$をタイヤ半径、$n$をギアの減速比、$m$を機体質量として、 $$ T = \frac{mra}{2n} $$ $$ \omega = \frac{60v}{2n\pi r} $$ となります。 $T$の式の分母に2が入っているのは、タイヤが二つで加速度が倍になるからです。
DCモーターSCR13-2005の特性
今回使用したDCモーターであるSCR13-2005の特性を見てみましょう。 シチズンマイクロ社から公開されているデータシートを見てみましょう。 これによるとトルク定数は $$ K_T = 4.49 [\mathrm{mNm/A}] $$ です。 先の変換式から逆起電力定数を計算すると $$ K_E = 0.470 [\mathrm{V/krpm}] $$ となります。単位の分母がkrpmになっていることに注意してください。 （余談ですがシチズンマイクロ社の担当の方に問い合わせたところ違う値を教えられました。どういうこと？）
フィードフォーワード制御を行ってみる
とりあえずフィードフォーワード制御のお試しということで、計算上$v = $1m/sの速度で定速運転をするときのデューティー比を与えてみましょう。 定速運転なので加速度$a=0$なので $$ r_D = \frac{60vK_E}{2n\pi rV_{bat}} = \frac{0.673 \times v}{V_{bat}}$$ この式に$v = 1$m/sを代入すると、例えばバッテリー電圧$V_{bat}=7.2$Vのときデューティー比は $r_D = 13.9\mathrm{\%}$となります。
(2021/05/08追記) 計算式を見返していたところ、タイヤ半径を入れるべきところに直径を入れてしまっていることを発見しました。 つまり係数は二倍の1.346となります。
実際にこの値をデューティー比としてモーターを動かしたのが以下の動画になります。 （バッテリー電圧は制御ループ内で測定して使っています。）
動画を見返すと、2秒時点から6秒時点まで4秒間でおよそ20回タイヤが回転しています。 タイヤ径が25mmなので空転状態で0.78m/sに相当する回転数です。 モーター自体に摩擦トルクがあること、ギアとタイヤのベアリングで摩擦が生じることを考えると、目標値の78%はまあまあ妥当な数字に思えます。今回はここまでです。次回はフィードバック制御を足すか、それとも摩擦トルクをフィードフォーワード制御に取り込むか、どちらかに仕様と思います。
参考資料
マイクロマウスシリーズ
comments powered by Disqus